常用的9个机器学习模型介绍
-

derekwh
2024-02-28 15:21:32
-
数据库开发技术
-
原创
机器学习在近年来广泛应用于各个领域。本文将将介绍9个机器学习常用模型的基本原理。1.线性回归
线性回归模型是一种用于预测连续型变量的机器学习模型,其基本原理是通过拟合线性关系来建立输入特征和输出变量之间的映射关系。基本原理
- 假设函数:线性回归假设输入特征与输出变量之间存在线性关系,可以用一个线性方程来描述。假设函数的形式为:Y = β0 + β1X1 + β2X2 + ... + βn*Xn,其中Y表示输出变量,Xi表示输入特征,βi表示对应特征的系数,β0表示截距。
- 损失函数:线性回归通过最小化损失函数来拟合模型。通常使用最小二乘法,即最小化观测值与模型预测值之间的差距的平方和。
- 模型训练:通过优化算法(如梯度下降法)迭代地调整模型参数,使得损失函数最小化。优化过程中,根据训练集的样本特征和对应的输出值,逐步更新模型中的系数和截距。
- 模型评估:使用测试集评估训练好的模型的性能,常用指标包括均方误差(MSE)、均方根误差(RMSE)和决定系数(R-squared)等。
实现步骤
- 准备数据集:收集及预处理训练数据,包括选择合适的特征、处理缺失值、处理异常值等。
- 拟合模型:根据选择的特征和目标变量,使用最小二乘法或其他优化算法来拟合线性回归模型。
- 模型评估:使用评估指标来评估模型的性能,并根据需要进行调整和改善模型。
- 模型应用:使用训练好的模型预测新的未知样本的输出值。
应用领域
金融领域:用于股票价格预测、房价预测、财务分析等。2.逻辑回归
逻辑回归是用于解决二分类问题的模型,通过将结果映射到一个概率值(0-1之间),并根据阈值进行分类。基于线性回归模型,使用sigmoid或softmax函数进行转换。实现原理
逻辑回归模型虽然名为“回归”,但实际上是一种分类模型。它的基本原理是在线性回归的基础上,通过一个激活函数(通常是sigmoid函数)将线性回归的连续值结果映射到0和1之间,从而完成分类任务。sigmoid函数的输出值可以被解释为某个样本属于正类的概率。实现步骤
- 数据准备:收集并预处理数据,包括特征选择、数据清洗、特征缩放等。
- 模型构建:定义逻辑回归模型,通常包括权重矩阵和偏置项。
- 损失函数选择:选择合适的损失函数,如交叉熵损失函数,来衡量模型预测与真实标签间的差异。
- 优化算法选择:选择合适的优化算法,如梯度下降法、随机梯度下降法或Adam等,用于迭代更新模型参数以最小化损失函数。
- 模型训练:通过迭代计算梯度并更新参数,直到损失函数收敛或达到预设的迭代次数。
- 模型评估:使用验证集或测试集评估模型的性能,如准确率、召回率等指标。
应用方向
逻辑回归模型在各个领域都有广泛的应用,包括但不限于:
- 医学领域:用于预测疾病的发生概率,如糖尿病、冠心病等。
- 金融领域:用于评估信用风险,如预测借款人是否违约。
- 市场营销:用于预测客户购买行为,如预测客户是否点击广告或购买产品。
- 社会学:用于分析社会现象,如预测个体是否选择进入劳动力市场。
优点:实现简单,计算量小,输出概率形式,易于解释预测结果。缺点:对于非线性问题拟合效果差,无法处理复杂的数据关系,对异常值敏感。3.决策树
决策树是一种树形结构的分类器,通过不断对特征进行划分,最终得到一系列决策规则。通过计算信息增益或基尼指数选择最优划分特征。模型原理
决策树模型利用概率论的原理,通过树形图作为分析工具进行决策分析。在决策树中,每个内部节点表示一个决策问题,每个分支代表一个可能的答案或解决方案,而每个叶节点则代表一个最终的结果或分类。决策树通过从根节点到叶节点的路径来模拟决策过程,并根据不同的条件选择相应的分支,最终得到决策结果。实现步骤
- 数据准备:收集并准备数据集,包括特征选择和数据清洗等。
- 构建决策树:从根节点开始,根据特征的重要性进行分裂,递归地构建决策树。通常使用信息增益、增益率或基尼指数等指标来选择最佳分裂特征。
- 剪枝:为防止过拟合,可以对决策树进行剪枝操作,包括预剪枝和后剪枝两种策略。预剪枝是在构建决策树的过程中提前停止树的生长,后剪枝是在决策树构建完成后进行修剪。
- 模型评估:使用验证集或测试集评估决策树的性能,如准确率、召回率等指标。
优缺点
决策树模型的优点包括直观易懂、可解释性强、能够处理非线性关系和非线性数据等。它还可以用于特征选择,帮助理解数据的内在结构和关系。然而,决策树模型也存在一些缺点,如容易过拟合、对连续型特征的处理能力较弱以及对缺失值的处理不够灵活等。4.随机森林模型
模型原理
随机森林是基于决策树的集成模型,通过构建多个决策树,并对结果进行综合,得到最终输出。实现步骤
- d. 建立随机森林模型,通过选择决策树个数和随机特征,利用投票或平均方式综合结果
优点:泛化能力强,处理高维数据和大数据集效果好,对噪声不敏感。缺点:模型解释性较弱,训练耗时长,需要较多的内存。随机森林广泛应用于图像处理、文本分类、金融风险评估等领域,以及特征选择和变量重要性评估。5.支持向量机
模型原理
支持向量机是一种二分类模型,通过寻找最优超平面将不同类别的样本分开。基于间隔最大化原则,通过核函数将样本映射到高维空间进行分类。实现步骤
- d. 建立支持向量机模型,选择核函数和正则化参数,用SMO等算法进行模型训练
优点:泛化能力强,可以处理高维数据,对噪声不敏感 。缺点:对大规模数据集的计算复杂度较高,需要调优参数。支持向量机广泛应用于文本分类、图像识别、生物信息学等领域,以及异常检测和回归问题。6.K近邻模型
模型原理
K近邻是一种基于实例的学习模型,通过计算距离度量找到与给定样本最相似的K个训练样本,根据多数投票结果进行分类。实现步骤
优点:思想简单,易于实现和理解,对样本分布无假设 。缺点:计算复杂度高,对异常值敏感,需要大量的存储空间。K近邻广泛应用于推荐系统、图像识别、异常检测等领域,以及基于相似性的分类问题。7.朴素贝叶斯模型
模型原理
朴素贝叶斯是一种基于贝叶斯定理的概率模型,通过学习训练样本的条件概率,对新样本进行分类。假设所有特征之间相互独立。朴素贝叶斯模型的核心是贝叶斯定理,它描述了在已知某些条件下,某个事件发生的概率。在朴素贝叶斯分类器中,“朴素”一词意味着它假设特征之间是相互独立的,这意味着一个特征的出现与否不依赖于其他特征。尽管这个假设在现实中往往不成立,但朴素贝叶斯分类器在很多情况下仍然表现良好。实现步骤
- 准备数据:收集并准备数据集,包括特征选择和数据清洗等。
- 计算先验概率:对于每个类别,计算训练数据集中该类别的样本所占的比例,这将成为该类别的先验概率。
- 计算条件概率:对于每个特征和每个类别,计算在给定类别下该特征出现的概率。这通常通过计算在某个类别中特定特征值的样本数量与该类别的总样本数量之比来完成。
- 分类:对于新的数据点,计算其在每个类别下的后验概率,这通常通过将先验概率与给定特征值的条件概率相乘来完成。然后,选择具有最大后验概率的类别作为预测类别。
优点:计算简单,对小规模数据效果好,对缺失数据不敏感 。缺点:假设特征之间独立,不适用于特征相关性较强的问题。朴素贝叶斯广泛应用于文本分类、垃圾邮件过滤、情感分析等领域,以及基于概率的分类问题。8.神经网络模型
模型原理
神经网络是由多个神经元相互连接的网络模型,通过前向传播和反向传播的方式进行学习。通过调整权重和偏置,逐渐优化模型。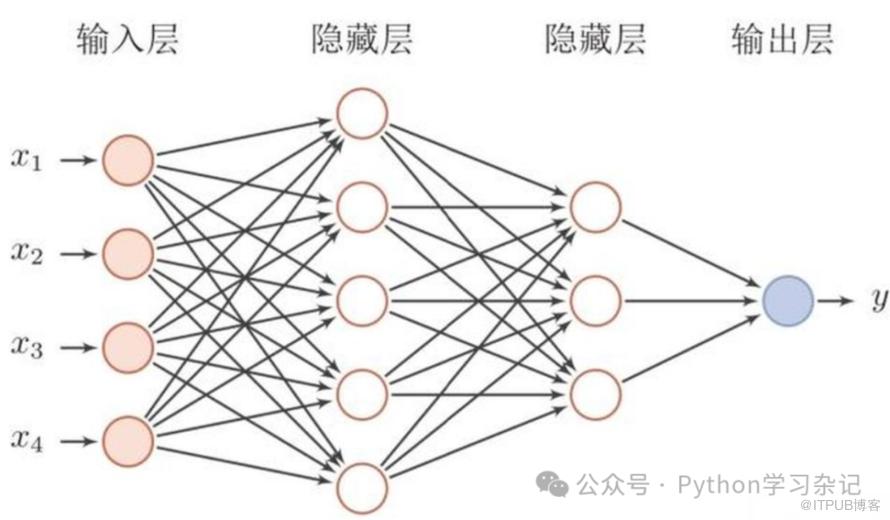
实现步骤
- d. 建立神经网络模型,选择网络结构、激活函数和优化方式
神经网络广泛应用于图像识别、语音识别、自然语言处理等领域,以及大规模数据的处理和深度学习任务。9.集成模型
模型原理
集成学习模型的基本原理是将多个弱学习器组合成一个强学习器,通过集体决策来提高模型的准确性和鲁棒性。其核心理念是“三个臭皮匠,顶个诸葛亮”,即通过结合多个模型的预测结果,来得到更加可靠、准确的预测结果。实现步骤
- 弱学习器训练:从原始数据集中采用不同的采样方法和特征选择方式,训练多个相对较弱的学习器。这些学习器可以是同一种类型的模型,也可以是不同类型的模型。
- 弱学习器预测:利用每个弱学习器对新样本进行预测,并得到一组预测结果。
- 集成学习器构建:根据一定的规则或算法,将多个弱学习器的预测结果进行集成,得到最终的集成学习器的预测结果。
常用的集成学习方法
- Bagging(装袋法):通过自助采样(bootstrap)的方式,从原始训练集中有放回地采样多个子训练集,每个子训练集对应一个弱学习器,然后将各个弱学习器的预测结果进行平均或投票得到最终结果。
- Boosting(提升法):通过迭代的方式,逐步调整样本的权重,使得每次迭代拟合的模型关注于之前错误分类的样本,从而得到一组弱学习器,然后将弱学习器进行加权组合得到最终结果。
- Random Forest(随机森林):通过合并多个决策树模型构建的集成模型,每个决策树都是通过随机选择特征子集和样本子集来进行训练。
集成学习模型应用
- 医疗领域:用于疾病诊断、药物研发、医疗图像分析等。
- 计算机视觉领域:用于目标检测、图像分类、人脸识别等。
- 自然语言处理领域:用于情感分析、文本分类、机器翻译等。
本文介绍了机器学习常用的十种模型的基本原理、实现过程、应用方向。若要进一步了解每个模型的应用,需要多花时间深入学习。








