混合整数规划(MIP)是一种优化算法,广泛应用于供应链、运输、制造等行业。它是在线性规划(LP)的基础上,增加了一些整数限制。这些限制使得问题更加复杂,但也能更好地建模实际问题。
MIP问题通常包括线性目标函数和一组线性约束条件,同时要求某些决策变量是整数。这些约束条件和决策变量的整数属性使得MIP问题难以求解。MIP问题的求解可以通过分支定界、割平面等方法来实现。本文将介绍MIP模型的基本概念、分类、求解方法和应用案例。
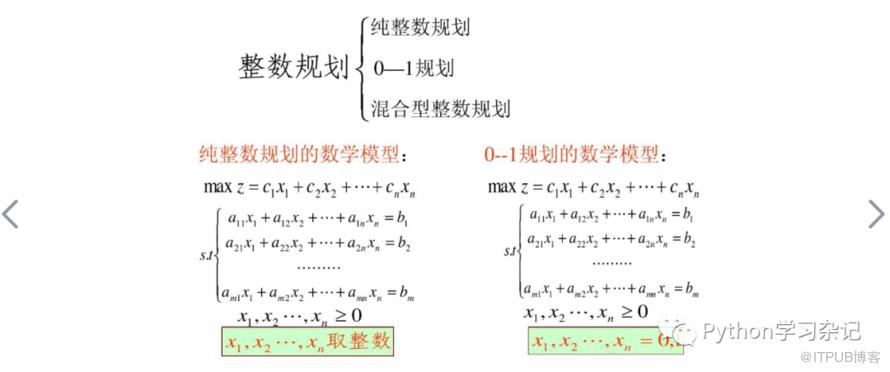
MIP模型基本概念
MIP模型是由线性约束条件、目标函数和决策变量组成的。其中,决策变量通常被限制为整数。MIP模型可以表示为以下数学公式:
max/min c'x
s.t. Ax <= b
x ∈ Z
其中,c是目标函数的系数向量,x是决策变量向量,A是约束条件的系数矩阵,b是约束条件的右侧向量。最后一个条件x ∈ Z表示决策变量是整数。MIP模型可以分为纯MIP和混合整数规划(MILP)。纯MIP是指所有决策变量都是整数,而MILP允许一些决策变量是实数。对于这些实数变量,我们可以通过线性规划来求解。MIP模型的约束条件和决策变量的整数属性使得其在实际问题中应用广泛,例如在物流和供应链管理中,MIP模型可以用于优化配送和库存管理,提高运输效率和减少成本。MIP模型的求解方法
MIP问题的求解可以通过分支定界、割平面等方法来实现。在这些方法中,分支定界是最常用的方法。
分支定界是将问题分成更小的子问题,然后递归地解决这些子问题。在每个子问题中,我们选择一个决策变量并将其分为两个部分:一个整数部分和一个非整数部分。然后我们分别解决这两个子问题,直到找到最优解或证明无解。
割平面是将原问题转化为一个线性规划问题,并添加一些附加约束条件。这些约束条件被称为割约束。割平面方法可以减少分支定界法中的分支数,从而提高求解效率。
除了分支定界和割平面外,MIP问题还可以通过混合整数线性规划(MILP)求解。MILP可以将MIP问题转化为一个线性规划问题,并使用分支定界和割平面来处理整数变量。
MIP模型的应用案例
供应链管理
在供应链管理中,MIP模型可以用于优化仓库的物流配送问题。例如,如何将仓库中的货物分配到不同的客户,以最小化物流成本和满足客户需求。另一个应用是优化供应链的库存管理。在实际应用中,随着供应链的复杂性增加,库存管理变得更加困难。MIP模型可以帮助企业更好地管理库存,以满足客户需求并减少成本。运输规划
在运输规划中,MIP模型可以用于优化货物的运输路径和运输方式。例如,在物流公司中,如何安排不同运输车辆的路线,以最小化成本和时间?另一个应用是优化交通运输网络。在大城市中,交通拥堵和道路状况的变化会给交通网络带来巨大的挑战。MIP模型可以帮助城市规划师更好地管理交通运输网络,以提高城市的运输效率和减少交通拥堵。
制造业
在制造业中,MIP模型可以用于优化生产流程和减少生产成本。例如,在汽车工厂中,如何安排生产线,以最大化生产效率和减少能源消耗?MIP模型还可以用于优化供应商选择。在制造业中,供应商选择是一个关键的决策,可以影响制造商的成本和生产效率。MIP模型可以帮助制造商更好地选择合适的供应商。MIP模型的优缺点
MIP模型的优点在于能够处理复杂的实际问题,并且可以用于多种领域,包括供应链、运输、制造等。此外,MIP模型还可以处理不同类型的约束条件,如等式约束、不等式约束等。MIP模型的缺点在于随着问题规模的增加,求解时间会变得非常长。此外,由于MIP问题是NP难问题,因此在某些情况下,可能无法找到最优解。为了解决这个问题,我们可以使用启发式算法、元启发式算法等方法。结论
混合整数规划是一种重要的优化算法,可以应用于许多领域。MIP模型的求解方法包括分支定界、割平面等。在实际应用中,我们需要根据具体问题选择适合的求解方法。希望本文能够帮助读者更好地理解MIP模型。未来发展
未来,MIP模型将继续发展并扩大其应用领域。随着新技术的出现,MIP模型将会变得更加高效和精确。例如,基于机器学习的MIP模型可以预测未来的需求和生产情况,并提前做好准备。此外,MIP模型还可以与其他优化算法结合使用,例如进化算法、遗传算法等,以提高求解效率。总之,MIP模型的未来发展充满着无限的可能性。

