pulp是一个Python库，用于创建和求解线性规划和整数规划问题。它提供了一个简洁的语法，可以方便地定义决策变量、目标函数和约束条件，并调用不同的求解器来得到最优解或可行解。pulp的主要特点有：

支持多种类型的决策变量，包括连续型、整数型、二进制型等。
支持多种内置或外部的求解器，包括CBC、GLPK、CPLEX、Gurobi等
支持导出和导入问题的LP格式或MPS格式支持基于字典或列表的创建规划问题，适用于大规模的问题。
支持对问题进行修改和重新求解，以实现灵活的建模 pulp可以用于解决各种实际应用中的优化问题，例如生产计划问题、运输分配问题等。

pulp基础介绍

用pulp定义一个简单的问题，需要以下几个步骤：

导入pulp模块创建一个LpProblem对象，
指定问题的名称和目标函数的方向（最大化或最小化）创建一些LpVariable对象，
指定变量的名称、类型和上下界
添加目标函数和约束条件到LpProblem对象中
调用solve方法求解问题，并打印结果
例如，如果你想求解这样一个线性规划问题，可以按照如下代码实现：

import pulp
# 创建一个问题，名为"example"，目标是最小化
prob = pulp.LpProblem('example', sense=pulp.LpMinimize)
# 创建两个变量，x和y，取值范围为[0, +∞)
x = pulp.LpVariable('x', lowBound=0)
y = pulp.LpVariable('y', lowBound=0)
# 添加目标函数
prob += x + 2 * y
# 添加约束条件
prob += x + y <= 4
prob += x - y >= 1
# 求解问题
status = prob.solve()
# 打印结果
print(pulp.LpStatus[status]) # Optimal
print(pulp.value(x)) # 1.5
print(pulp.value(y)) # 2.5
print(pulp.value(prob.objective)) # 6.0

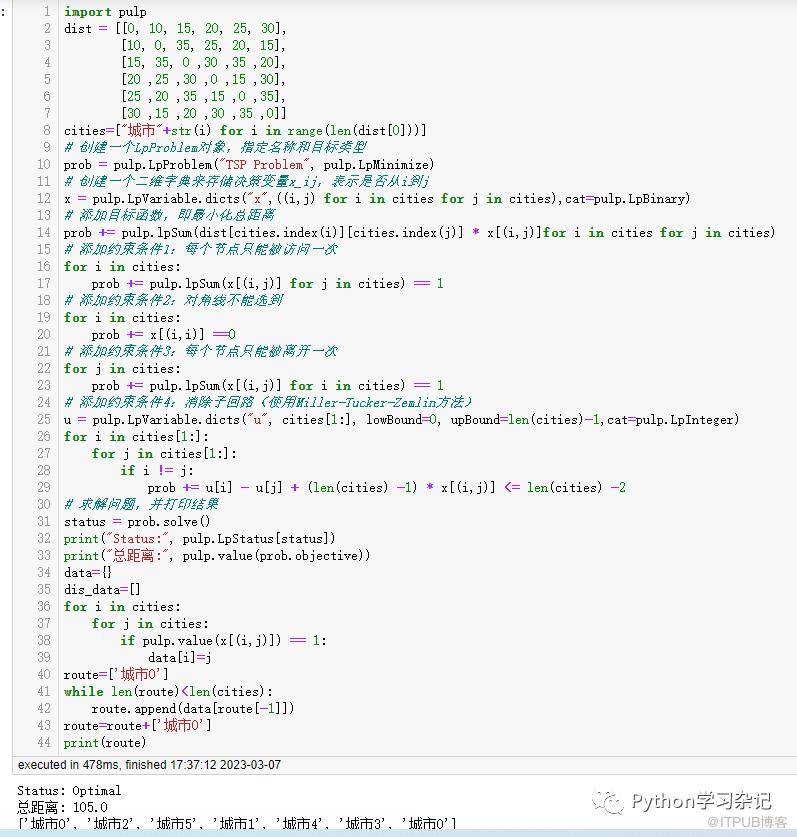
pulp解决TSP问题

TSP也可以按照混合整数规划来建模，其建模是一个比较复杂的例子。对于小规模TSP问题,pulp可以快速求解。

TSP问题介绍

TSP问题，即旅行商问题，是数学领域中著名的组合优化问题之一。它的问题原型是：有一个旅行商要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是使总的旅行距离或花费最小。

TSP问题可以用图论来表示：给定一个带权完全无向图，其中顶点表示城市，边表示两个城市之间的距离或花费，求一个权值最小的哈密尔顿回路。

TSP问题是一个NP完全问题，也就是说没有已知的多项式时间算法可以解决它。因此，在实际应用中，大规模TSP问题，人们通常采用启发式算法或近似算法来寻找较优或次优解；小规模TSP问题可以用精确算法求解。

以下介绍TSP问题用pulp搭建模型的基本求解步骤。

导入基础数据

# 导入pulp库
import pulp
# 定义城市节点和距离矩阵
dist = [[0, 10, 15, 20, 25, 30],
        [10, 0, 35, 25, 20, 15],
        [15, 35, 0 ,30 ,35 ,20],
        [20 ,25 ,30 ,0 ,15 ,30],
        [25 ,20 ,35 ,15 ,0 ,35],
        [30 ,15 ,20 ,30 ,35 ,0]]
cities=["城市"+str(i) for i in range(len(dist[0]))]

设定变量和目标

# 创建一个LpProblem对象，指定名称和目标类型
prob = pulp.LpProblem("TSP Problem", pulp.LpMinimize)
# 创建一个二维字典来存储决策变量x_ij，表示是否从i到j
x = pulp.LpVariable.dicts("x",((i,j) for i in cities for j in cities),cat=pulp.LpBinary)
# 添加目标函数，即最小化总距离
prob += pulp.lpSum(dist[cities.index(i)][cities.index(j)] * x[(i,j)]for i in cities for j in cities)

约束条件1：每个节点只能被访问一次

# 添加约束条件1：每个节点只能被访问一次
for i in cities:
    prob += pulp.lpSum(x[(i,j)] for j in cities) == 1

约束条件2：对角线不能选到

# 添加约束条件2：对角线不能选到
for i in cities:
    prob += x[(i,i)] ==0

约束条件3：每个节点只能被离开一次

# 添加约束条件3：每个节点只能被离开一次
for j in cities:
    prob += pulp.lpSum(x[(i,j)] for i in cities) == 1

约束条件：消除子回路（MTZ方法）

# 添加约束条件4：消除子回路（使用Miller-Tucker-Zemlin方法）
u = pulp.LpVariable.dicts("u", cities[1:], lowBound=0, upBound=len(cities)-1,cat=pulp.LpInteger)
for i in cities[1:]:
    for j in cities[1:]:
        if i != j:
            prob += u[i] - u[j] + (len(cities) -1) * x[(i,j)] <= len(cities) -2

求解，并整理打印结果

# 求解问题，并打印结果
status = prob.solve()
print("Status:", pulp.LpStatus[status])
print("总距离:", pulp.value(prob.objective))
data={}
dis_data=[]
for i in cities:
    for j in cities:
        if pulp.value(x[(i,j)]) == 1:
            data[i]=j
route=['城市0']
while len(route)    route.append(data[route[-1]])    
route=route+['城市0']
print(route)

完整代码

导入pulp库
import pulp
# 定义城市节点和距离矩阵
dist = [[0, 10, 15, 20, 25, 30],
        [10, 0, 35, 25, 20, 15],
        [15, 35, 0 ,30 ,35 ,20],
        [20 ,25 ,30 ,0 ,15 ,30],
        [25 ,20 ,35 ,15 ,0 ,35],
        [30 ,15 ,20 ,30 ,35 ,0]]
cities=["城市"+str(i) for i in range(len(dist[0]))]
# 创建一个LpProblem对象，指定名称和目标类型
prob = pulp.LpProblem("TSP Problem", pulp.LpMinimize)
# 创建一个二维字典来存储决策变量x_ij，表示是否从i到j
x = pulp.LpVariable.dicts("x",((i,j) for i in cities for j in cities),cat=pulp.LpBinary)
# 添加目标函数，即最小化总距离
prob += pulp.lpSum(dist[cities.index(i)][cities.index(j)] * x[(i,j)]for i in cities for j in cities)
# 添加约束条件1：每个节点只能被访问一次
for i in cities:
    prob += pulp.lpSum(x[(i,j)] for j in cities) == 1
# 添加约束条件2：对角线不能选到
for i in cities:
    prob += x[(i,i)] ==0 
# 添加约束条件3：每个节点只能被离开一次
for j in cities:
    prob += pulp.lpSum(x[(i,j)] for i in cities) == 1
# 添加约束条件4：消除子回路（使用Miller-Tucker-Zemlin方法）
u = pulp.LpVariable.dicts("u", cities[1:], lowBound=0, upBound=len(cities)-1,cat=pulp.LpInteger)
for i in cities[1:]:
    for j in cities[1:]:
        if i != j:
            prob += u[i] - u[j] + (len(cities) -1) * x[(i,j)] <= len(cities) -2
# 求解问题，并打印结果
status = prob.solve()
print("Status:", pulp.LpStatus[status])
print("总距离:", pulp.value(prob.objective))
data={}
dis_data=[]
for i in cities:
    for j in cities:
        if pulp.value(x[(i,j)]) == 1:
            data[i]=j
route=['城市0']
while len(route)    route.append(data[route[-1]])    
route=route+['城市0']
print(route)

如果城市变多，试一试看看代码运行时间，城市调整到17个，距离矩阵更新成17*17。data换成以下数据。

dist = [[0, 548, 776, 696, 582, 274, 502, 194, 308, 194, 536, 502, 388, 354,468, 776, 662],
[548, 0, 684, 308, 194, 502, 730, 354, 696, 742, 1084, 594, 480, 674,1016, 868, 1210],
[776, 684, 0, 992, 878, 502, 274, 810, 468, 742, 400, 1278, 1164,1130, 788, 1552, 754],
[696, 308, 992, 0, 114, 650, 878, 502, 844, 890, 1232, 514, 628, 822,1164, 560, 1358],
[582, 194, 878, 114, 0, 536, 764, 388, 730, 776, 1118, 400, 514, 708,1050, 674, 1244],
[274, 502, 502, 650, 536, 0, 228, 308, 194, 240, 582, 776, 662, 628,514, 1050, 708],
[502, 730, 274, 878, 764, 228, 0, 536, 194, 468, 354, 1004, 890, 856,514, 1278, 480],
[194, 354, 810, 502, 388, 308, 536, 0, 342, 388, 730, 468, 354, 320,662, 742, 856],
[308, 696, 468, 844, 730, 194, 194, 342, 0, 274, 388, 810, 696, 662,320, 1084, 514],
[194, 742, 742, 890, 776, 240, 468, 388, 274, 0, 342, 536, 422, 388,274, 810, 468],
[536, 1084, 400, 1232, 1118, 582, 354, 730, 388, 342, 0, 878, 764,730, 388, 1152, 354],
[502, 594, 1278, 514, 400, 776, 1004, 468, 810, 536, 878, 0, 114,308, 650, 274, 844],
[388, 480, 1164, 628, 514, 662, 890, 354, 696, 422, 764, 114, 0, 194,536, 388, 730],
[354, 674, 1130, 822, 708, 628, 856, 320, 662, 388, 730, 308, 194, 0,342, 422, 536],
[468, 1016, 788, 1164, 1050, 514, 514, 662, 320, 274, 388, 650, 536,342, 0, 764, 194],
[776, 868, 1552, 560, 674, 1050, 1278, 742, 1084, 810, 1152, 274,388, 422, 764, 0, 798],
[662, 1210, 754, 1358, 1244, 708, 480, 856, 514, 468, 354, 844, 730,536, 194, 798, 0]]

不到1秒就能求解，求解速度还可以。如果TSP模型的城市数量继续增加，可能pulp无法短时间内求解，后续大家可以尝试其他启发式方法。

Pulp求解TSP问题介绍及程序实现