点击上方蓝字加入我们

本系列文章是原作者Rohit Patel的长篇雄文《Understanding LLMs from Scratch Using Middle School Math-A self-contained, full explanation to inner workings of an LLM》的深度学习与解读笔记。本篇是系列第七篇。我们强烈建议您在开始前阅读并理解前文（点击下方目录）。

1. 一个简单的神经网络

2. 这些模型是如何被训练的？

3. 这些模型如何生成语言？

4. 嵌入（Embeddings）

5. 子词分词器（Sub-word tokenizers）

6. 自注意力机制（Self-attention）

7. Softmax

8. 残差连接（Residual connections）

9. 层归一化（Layer Normalization）

10. Dropout

11. 多头注意力（Multi-head attention）

12. 位置嵌入（Positional embeddings）

13. GPT 架构

14. Transformer 架构

7

Softmax函数 - “概率”的起源

LLM本质上是一个基于概率输出的神经网络模型。但这里的“概率”来自哪里？今天我们就来说说语言模型中一个重要的角色：Softmax函数。（相信我，本文真的只需要初等函数知识）

01

困境来自哪里？

之前我们假设了一个神经网络，它的任务是输入一组特征数据，输出预测结果。预测的方式是从一组输出神经元中选择值最高的那个神经元。

比如，我们让神经网络预测是“叶子”还是“花”，最后的输出是两个数字，分别代表它认为“叶子”和“花”是正确答案的信心，假设是 (5, 1)。也就是神经网络认为它更倾向于选择“叶子”，因为 5 比 1 大。

一切似乎工作的很好，但有一个问题：

我们需要根据神经网络的输出与期望的理想值之间的差距（损失）来迭代调整模型参数（还记得梯度下降吗），不断的最小化损失（让模型预测得越来越准）。但这个“期望的理想值”应该是多少呢？应该是10还是100？当然最好是无穷大，但这样每次计算出的损失就也是无穷大，也就永远无法降低！

容易想到的解决办法是：把这个最大的“理想值”设定为固定值，比如“1”。现在每次输出只需要与这个固定值来比较，就可以计算损失。

02

为什么需要“概率”？

现在我们有了一个输出的“标杆”，一个固定的理想值：“1”。但仍然有一个问题，比如上面例子中的两次预测结果：

一次输出（5，1），选择更大的5，对应了“叶子”，假设这是正确的；

一次输出（0，1），选择更大的1，对应了”花“，这是错误答案；

现在我们要计算损失。把输出值与理想值（因为期望输出叶子，所以理想值是【1，0】）比较，显然第一次的（5，1）偏离更大，第二次的（0，1）偏离更小（实际上的损失计算当然不是这么简单），也就是：预测正确的第一种情况计算的损失反而更大！

所以，这里需要一个数学上的方法，它具有这样的作用：能够把一组任意数值对应到介于0-1之间的数，且总和为1，也就是“概率”。类似于一个函数：

比如把（5，1）转化为（0.83，0.17）,既没有改变原义；又易于理解（选择叶子的概率为0.83）；同时永远不会超过理想值（“1”）。

这个数学上的方法就是Softmax函数。

03

Softmax函数如何工作？

Softmax 是一个数学函数，它的作用就是将神经网络的一组输出转化成概率分布，这样就能清晰地知道神经网络选择每个选项的可能性。它的数学形式为：

Z_i是第i个选项的原始分数，n是选项的总数。

Softmax的数学特性可以确保三个重要特征：

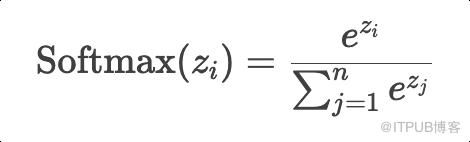
所有概率值都在 (0,1) 之间。
所有概率值的总和严格等于 1。
原始分值的大小关系被保留（即分数高的选项概率一定更高）。

我们以三个候选词的分值分别为（2，1，0.1）举例，它的计算过程如下：

1. 对每个分数做指数运算：

e² ≈ 7.389
e¹ ≈ 2.718
e⁰·¹ ≈ 1.105

为什么必须用指数函数？

差异放大：能够放大决策信号
正数保障：无论输入正负，结果永远为正
单调性：能够保持原来数值的大小顺序

还有一个特征，暂时我们知道就好：由于e指数函数的导数等于其自身，反向传播时能简化梯度计算。

2. 归一化计算概率：

将指数计算后的值相加：

7.389+2.718+1.105≈11.212

那么每个值的概率就是：

“2”的概率：7.389/11.212 ≈ 65.9%
“1”的概率：2.718/11.212 ≈ 24.2%
"0.1"的概率：1.105/11.212 ≈ 9.9%

很显然，这样计算的结果一定小于1，且总和严格等于1，符合概率要求

04

Softmax函数的价值

截至目前，我们已经知道Softmax在语言模型中的两个典型应用：输出层预测与注意力机制（计算注意力权重）。

是否还有其他意义呢？

Softmax把神经网络的输出转化为概率，而不是直接选择最高分的那个选项。更大的价值是：让模型在生成过程中可以根据概率探索更多样的可能。

1. 简单决策的问题

假设模型正在逐字符生成"Humpty Dumpty"这个词组，当前已经生成了"Humpty Du"，接下来需要预测下一个字符。模型的计算结果可能是：

"m"：得分较高（例如0.45）
"u"：得分最高（例如0.5）
其他字符（如"a", "b"等）：得分极低（例如0.05）

如果模型直接选择得分最高的"u"，那么生成的文本会变成"Humpty Duu..."，这显然是一个错误的路径，因为"Humpty Duu"并不是一个有效的词组。此时，模型的生成任务可能会陷入困境，因为后续的字符预测也会变得困难。

2. Softmax的灵活决策

Softmax的作用在于，它不会让模型盲目地选择得分最高的选项，而是根据得分分配概率。例如：

"u"：50%的概率
"m"：45%的概率
其他字符：5%的概率

这样，模型有接近一半的概率会选择"m"，从而生成正确的"Humpty Dumpty"。即使模型一开始选择了错误的"u"，它也有机会在后续的生成过程中回溯并修正错误。

所以，Softmax通过赋予次优选项一定的概率，使得模型能够在生成过程中进行探索。不过，这也是语言模型“不确定性”的来源，因为它总是在“探索”不同概率下的可能性。

05

一个熟悉的参数：温度(Temperature）

很多人会比较熟悉这个参数，用来控制文本输出结果的特征。这是怎么实现的呢？

其实温度就是在Softmax中引入一个参数：

这个参数T用来控制转化后的概率的结果。简单的说就是：

低温（T较小）：Softmax输出的概率分布更尖锐，模型更倾向于选择得分最高的选项，生成结果更确定，更保守，多样性较低。
高温（T较大）：Softmax输出的概率分布更平缓与均匀，模型更愿意尝试多样化的选项，生成结果更具创造性。

这就好比你在选择外卖，如果两家餐厅的评分为5分和1分，你会毫不犹豫的选择5分的；而如果它们的评分分别为4.9和4.7,你可能更愿意轮流尝试不同的餐厅。

以上就是Softmax函数的介绍，虽然易于理解，但却意义重大，是语言模型生成时的“决策导航仪”。通过概率转化，Softmax赋予了语言模型一种"智慧"：在犯错时有机会修正，在探索时保持多样性。

欢迎继续关注下一期，喜欢就点个赞吧！

THE END

福利时间

为了帮助LLM开发人员更系统性与更深入的学习RAG应用，特别是企业级的RAG应用场景下，当前主流的优化方法与技术实现，我们编写了《基于大模型的RAG应用开发与优化 — 构建企业级LLM应用》这本长达500页的开发与优化指南，与大家一起来深入到LLM应用开发的全新世界。

更多细节，点击链接了解

交流请识别以下名片

中学生就能看懂：从零开始理解LLM内部原理【七】｜ “概率”从哪里来？

1. 简单决策的问题