本系列文章是原作者Rohit Patel的长篇雄文《Understanding LLMs from Scratch Using Middle School Math-A self-contained, full explanation to inner workings of an LLM》的深度学习与解读笔记。本篇是系列第二篇。我们强烈建议您在开始前阅读并理解前文:6. 子词分词器(Sub-word tokenizers)7. 自注意力机制(Self-attention)9. 残差连接(Residual connections)10. 层归一化(Layer Normalization)12. 多头注意力(Multi-head attention)13. 位置嵌入(Positional embeddings)在上一篇的简单神经网络中,为了让这个魔力“盒子”能够接收我们输入的数值(代表颜色的RGB值与体积Vol值),并输出期望的信息(叶子还是花的概率),我们假设已经“神奇的”得到了能够生成合理输出的模型权重(神经元连线上的数字,也被称为模型的参数):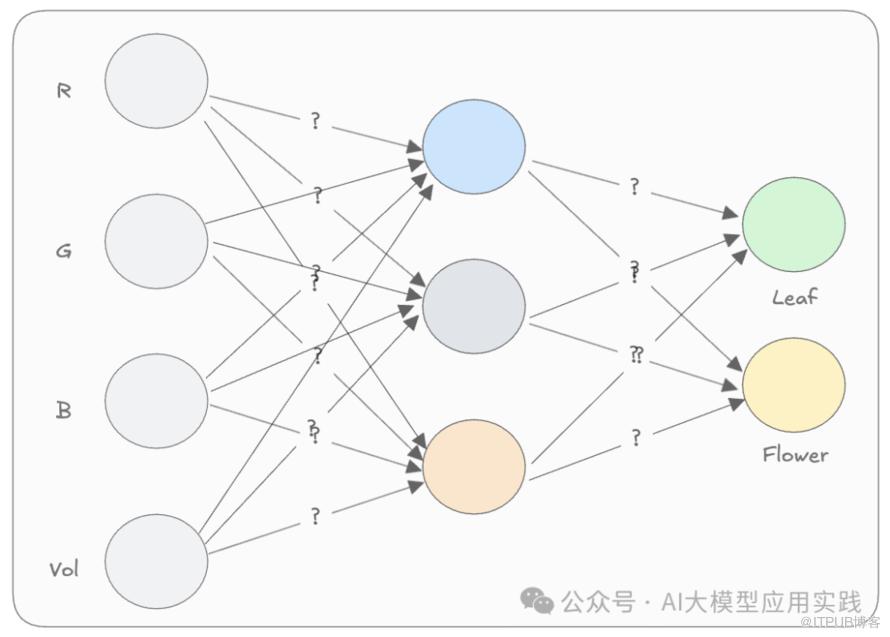
用来识别“叶子”与“花”的简单神经网络
那么,这些权重是怎么确定的呢?
其实,这些权重是通过一个叫做“训练”的过程来确定的,而这个过程需要使用一些“训练数据”,也就是“投喂”给模型用来学习的知识。
现在假设我们有一组针对这个神经网络的训练数据:其中包含输入数据及其对应的叶子或花的标签。因为每组数据(R, G, B, Vol)都已经明确标注了它是“leaf”还是“flower”,所以这是一种“有标注的数据”:
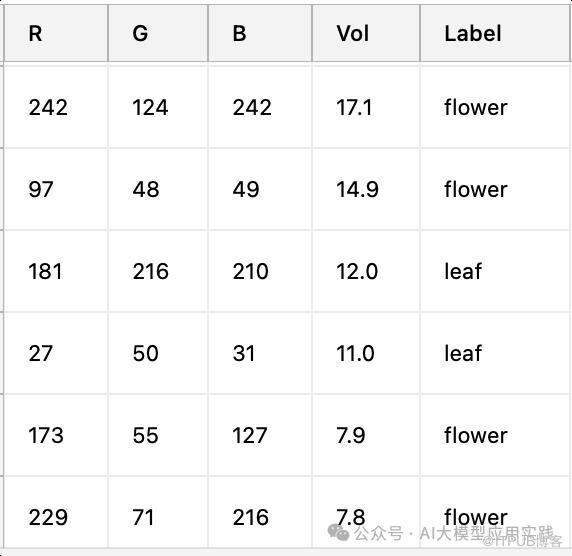
一组标注的用来训练神经网络的数据
下面是你可以看懂的模型训练的具体过程。记住,训练的目的是为了确定“权重”:我们从随机数开始。也就是说,将每个权重初始化为一个随机值。比如像下图,这里的连线上的权重数字都是随机生成(图中未列全):
给神经网络设置随机的权重
以一组标注为“叶子”的输入数据为例:R = 181, G = 216, B = 210, Vol = 12.0我们的目标是让模型的输出层中表示“叶子”概率的神经元数值更大。例如,希望叶子的输出为 1,而花的输出为 0。
由于当前模型的参数是随机的,因此输出数值可能并不符合我们的预期。假设模型输出为 0.6(叶子)和 0.4(花)。如下:
初始权重下的输出结果
由于这里输出层的结果(0.6,0.4)与我们期望的结果(1,0)并不一样。所以用一个数值来衡量当前输出与期望输出的差距,也就是损失(loss)。计算损失的方法是“损失函数”,这里用最简单的计算方法:
损失 = |1 - 0.6| + |0 - 0.4| = 0.4 + 0.4 = 0.8很显然,损失值越小,代表模型输出越接近我们期望的结果。而训练模型的目标就是“最小化损失”。为了最小化损失,我们需要调整模型的权重,也就是图中连线上的数字,看看增加或减少它是否会使损失变小。比如在上面例子中:当前某权重为 0.17,输出层的叶子值比期望值低,且叶子的神经元值是正数。现在我们尝试调整:
-
将这个权重增加到 0.18,重新输出并计算损失。观察是否损失减小。如果减小了,说明增加这个权重是正确方向。
当然在实际训练中不会每次只调整一个权重。通过这样反复多轮的调整,将所有的权重不断的稍做增大或者减小,最终损失就会降低。这是权重调整的最简单描述,但实际训练中要复杂的多,你还需要理解几个概念:
在实际训练时,不可能是这样“摸索”式的、无方向的调整。每次调整权重你需要知道:
比如把某个权重0.17应该调整到0.18还是0.16?
这决定了把某个权重0.17调整到0.18,还是调整到1.8?在神经网络中,用“梯度”这个概念来帮助调整权重。权重的梯度就是用来衡量损失相对于神经网络中该权重的变化方向与变化率。也就是:当改变这个权重时,损失会增大还是减小,及其变化得有多块。比如,某两个权重的梯度分别为+100,-20,意味着增大第一个权重会使得损失变大,增大第二个权重则会使损失变小;且第一个权重调整时,损失变化的更快。有了”梯度“这个帮手,现在调整权重是不是就有了方向感与尺度感?现在我们可以方便的调整权重:你只需要根据梯度指引的方向,根据一定的算法把所有权重向使得损失减小的方向调整。这种通过梯度来调整权重(参数),让损失不断变小的方法称为梯度下降(Gradient Descent),而这里的优化算法就是梯度下降算法。简单说,梯度下降算法就是一个根据旧权重与梯度来生成新权重的公式。即:新权重 = 旧权重 - 学习率 * 权重对应梯度(学习率是一个控制调整步幅的值)现在假设某个权重是0.17,梯度是200,学习率0.01,那么计算出的新权重:新权重 = 0.17 - 0.01 * 200 = -1.83把这个新权重更新到模型,准备开始下一轮的训练过程。梯度是在每次权重更新后,根据最后输出结果的损失值,沿着神经网络方向“逆流而上”,根据特定的算法分析每一层对损失的影响,得到每个权重的梯度值。这一部分的算法在此不做深入,不影响后续的理解。每次更新所有权重后,我们重新计算输出与损失,并再次调整权重。随着多次迭代(即“训练”),损失会逐渐减小,模型的参数趋于合理。通常,完整训练一个数据集的过程称为 一个周期(epoch)。通过多次周期训练,就可以让模型在整个训练集上表现良好。以上就是一个神经网络模型的训练过程,用下图做个总结:
- 前向传播(Forward Propagation):输入数据送入神经网络,输出结果
- 计算损失(Loss Calculation):通过损失函数计算输出结果与期望的差异
- 反向传播(Backward Propagation):计算损失关于参数(权重与偏置)的梯度
-
参数更新(Parameter Update):根据梯度下降算法更新训练参数
上面计算损失时,我们都是用一个样本举例。但实际上模型训练中会涉及大量训练样本时,每个样本的损失可能并不一致。例如,模型对样本 A 的预测可能很好,但对样本 B 的预测误差很大。如果只根据某一个样本调整权重,会导致对其他样本的预测变差。为了克服这一问题,通常定义 平均损失(Average Loss),即对所有训练样本的损失求平均值。训练过程中,我们通过优化平均损失,确保模型在整体上对所有样本表现更好,而不仅仅对单个样本。假设有 3 个样本,其损失分别为 0.2、0.5 和 0.1,则平均损失为:通过梯度下降算法,我们根据平均损失调整权重,既能降低高损失样本的误差,也能维持低损失样本的准确性,从而能使模型在整个数据集上有更均衡的表现。在实际操作中,训练深度神经网络是一个艰难且复杂的过程,因为在训练过程中,梯度很容易失控(特别是在非常深的神经网络中)。
- 权重梯度可能会变得非常小(梯度消失):导致权重无法根据梯度做更新。
-
权重梯度也可能非常大(梯度爆炸):权重变化时导致损失变化过于剧烈。
梯度消失与梯度保障会导致训练不稳定。实际应用中,会通过改进的损失计算函数、激活函数(参考第一节内容)等方法来改进,暂时你只需要知道这个问题的含义即可。下一篇我们将看到神经网络如何用来生成“语言”,而不只是识别“叶子”和“花”。
为了帮助LLM开发人员更系统性与更深入的学习RAG应用,特别是企业级的RAG应用场景下,当前主流的优化方法与技术实现,我们编写了《基于大模型的RAG应用开发与优化 — 构建企业级LLM应用》这本长达500页的开发与优化指南,与大家一起来深入到LLM应用开发的全新世界。更多细节,点击链接了解
此处购买享5折优惠








